Intro
After Implicit-Decoder part 1 – 3D reconstruction this time talking about 3D generation and limitations for deep learning and 3D.
3D generation

Remember GANs? Well, this same technique can be used to generate the airplanes you see to the left.
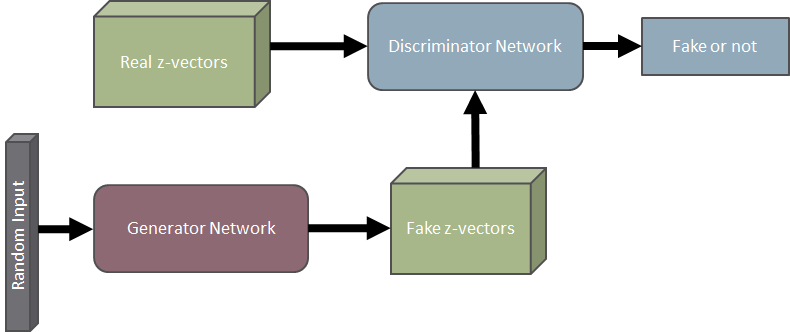
How does it happen? The trick is to use the same decoder network seen below. Specifically the same decoder that was trained along with the encoder. What happens is that we train a GAN network to generate a fake z-vector.
The discriminator gets as input real z-vectors from the encoder-decoder network along with fake z-vectors from the generator network. The generator network is trained to only produce new z-vectors based on a random input. Since the decoder knows to get as input a z-vector and from it reconstruct a 3D model and the generator is trained to produce z-vectors which resemble real ones, new 3D models can be reconstructed using both networks combined.
Also, we can see that the gif shows one airplane model morphing into a new one. This is done by taking the z-vectors for the first and last 3D models, let’s call these vectors z_start and z_end, then new z-vectors are calculated as a linear combination pf z_start and z_end. Specifically, a number (let’s say alpha) between 0 and 1 is picked and then a new z – z_new is calculated: z_new = (z_start*alpha + z_end*(1-alpha)). Then z_new is fed into the decoder network and the interim 3D models can be calculated.
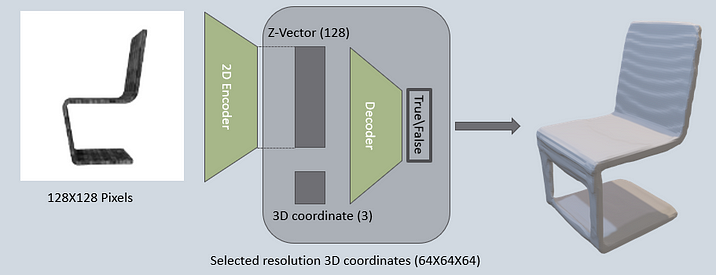
The reason that there is such a smooth transition between the different 3D models is that the implicit-decoder network is trained to recognize underlying 3D constructs of models based on z-vector, and more specifically, models in a specific model category. Therefore, a small change in z_vector will lead to a small change of the 3D model but still keep the 3D structure of the model category, that way it is possible to continuously change the model from z_start to z_end.
Limitations of deep learning and 3D reconstruction\generation
These results are brought here and other places make neural networks seem to be all-capable, easy to use and generalize to other scenarios, use cases and products. Sometimes this is the case, but many times it is not. In 3D generation and reconstruction there are limitations with neural networks. To name a few:
Dataset limitations
As we have demonstrated, the neural network requires training each time for a specific model category. There need to be enough models (usually minimum hundreds) in each category and enough categories to allow for any type of real life application of this type of neural network, ShapeNet are doing this work for the academic world and even there the amounts of categories and models in every category is limited. To make it commercially viable, we will need more models and categories. Also, each model needs to be labeled to its’ exact category, needs to be aligned translated and scaled accurately, needs to be saved in the right format. In addition, for each model we need images from different angles, different lighting positions and camera parameters, different scales alignments and translations. Again, ShapeNet and other research initiatives help with building this in order to help scientific progress. But, this also means there is a lot of overhead in dataset creation and processing in order to make this research into a product.
Accuracy Measures
A recurring question is how accurate is the 3D reconstruction or generation. A response question to this is – how do you measure accuracy in 3D reconstruction? Let’s say a human 3D designer reconstructs a 3D model from an image, how can we say if his work is accurate or not? Even if we have the original 3D model, how can we say that two 3D models are similar, or that the reconstructed 3D model is similar to the origin, and how can we quantify this similarity?The old school methods, such as MSE, IoU, F1 score, Chamfer and Normal distance [[Add reference – https://2d3d.ai/index.php/2019/10/09/3d-scene-reconstruction-from-single-image/]] are straightforward measures that don’t account for the 3D structure of the object. For example, IoU checks how much of the volume of a reconstructed 3D shape overlaps with the original 3D shape in comparison to the joint volume of both shapes. If the reconstructed shape is moved to be in a different volume in space, the IoU might be zero (because there is no overlap) even if the shapes are identical.
In the implicit decoder paper, the authors use a different measure of 3D shape similarity – LFD. This measure is invariant to scale of model, alignment and position (translation). The basic idea is to take 10 silhouette images of the model from angles on a dodecahedron and 10 different dodecahedrons per model.

Then, when comparing between two models, compare the visual similarity of the images from these 10 dodecahedrons using Fourier and Zernike coefficients.
References
- Implicit Decoder: Chen, Zhiqin, and Hao Zhang. “Learning implicit fields for generative shape modeling.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.
- Shapenet: https://www.shapenet.org/
- LFD: Chen, Ding‐Yun, et al. “On visual similarity based 3D model retrieval.” Computer graphics forum. Vol. 22. No. 3. Oxford, UK: Blackwell Publishing, Inc, 2003.

1 comment
[…] Implicit-Decoder part 2 – 3D generation […]